Posts Tagged ‘quintics’

23 Jul

Hypergeometric formulas for Ramanujan’s continued fractions 2

Posted by tpiezas in complex analysis, geometry, identities. Tagged: , , , .

(continued from yesterday’s post)

III. Icosahedral group

Given the Rogers-Ramanujan identities (see also here),

\begin{aligned} G(q) &= \sum_{n=0}^\infty \frac{q^{n^2}}{(q;q)_n} = \prod_{n=1}^\infty \frac{1}{(1-q^{5n-1})(1-q^{5n-4})}\\H(q) &= \sum_{n=0}^\infty \frac{q^{n^2+n}}{(q;q)_n} = \prod_{n=1}^\infty \frac{1}{(1-q^{5n-2})(1-q^{5n-3})}\end{aligned}

I observed that,

\begin{aligned}&q^{-1/60}G(q) = j^{1/60}\,_2F_1\big(\tfrac{19}{60},\tfrac{-1}{60},\tfrac{4}{5},\tfrac{1728}{j}\big) = (j-1728)^{1/60}\,_2F_1\big(\tfrac{29}{60},\tfrac{-1}{60},\tfrac{4}{5},\tfrac{1728}{1728-j}\big)\\[2.5mm]&q^{11/60}H(q) = j^{-11/60}\,_2F_1\big(\tfrac{31}{60},\tfrac{11}{60},\tfrac{6}{5},\tfrac{1728}{j}\big) = (j-1728)^{-11/60}\,_2F_1\big(\tfrac{41}{60},\tfrac{11}{60},\tfrac{6}{5},\tfrac{1728}{1728-j}\big)\end{aligned}

where, as in the previous post, j=j(\tau) is the j-function, q = e^{2\pi i \tau} = \exp(2\pi i \tau), \tau = \sqrt{-N}, and N>1.  Since it is known that,

\begin{aligned}&r(q) = \cfrac{q^{1/5}}{1 + \cfrac{q}{1 + \cfrac{q^2}{1 + \cfrac{q^3}{1 + \ddots}}}} = \frac{q^{11/60}H(q)}{q^{-1/60}G(q)} = \frac{q^{11/60}\prod_{n=1}^\infty \frac{1}{(1-q^{5n-2})(1-q^{5n-3})}}{q^{-1/60}\prod_{n=1}^\infty \frac{1}{(1-q^{5n-1})(q^{5n-4})}}\end{aligned}

this implies that,

\begin{aligned}r(q) &=\frac{j^{-11/60}\,_2F_1\big(\frac{31}{60},\frac{11}{60},\frac{6}{5},\frac{1728}{j}\big) }{j^{1/60}\,_2F_1\big(\frac{19}{60},\frac{-1}{60},\frac{4}{5},\frac{1728}{j}\big)}\\[3mm]&=\frac{(j-1728)^{-11/60}\,_2F_1\big(\frac{41}{60},\frac{11}{60},\frac{6}{5},\frac{1728}{1728-j}\big) }{(j-1728)^{1/60}\,_2F_1\big(\frac{29}{60},\frac{-1}{60},\frac{4}{5},\frac{1728}{1728-j}\big)}\end{aligned}

Example. Let \tau = \sqrt{-4}, hence j = j(\sqrt{-4}) = 66^3. Then,

1/r(q) -r(q) = \left(\frac{1+\sqrt{5}}{2}\right)^4+\left(\frac{1+\sqrt{5}}{2}\right)5^{3/4} = 12.2643\dots

Furthermore, since Ramanujan established that,

G(q^{11})H(q)-q^2G(q)H(q^{11}) = 1

if we define the two functions,

\begin{aligned}U(\tau) &= \big(j(\tau)\big)^{1/60}\,_2F_1\big(\tfrac{19}{60},\tfrac{-1}{60},\tfrac{4}{5},\tfrac{1728}{j(\tau)}\big)\\V(\tau) &= \big(j(\tau)\big)^{-11/60}\,_2F_1\big(\tfrac{31}{60},\tfrac{11}{60},\tfrac{6}{5},\tfrac{1728}{j(\tau)}\big) \end{aligned}

then the counterpart hypergeometric identity is also beautifully simple and given by,

U(11\tau)V(\tau)-U(\tau)V(11\tau)=1

In the next post, we will use one of the hypergeometric formulas to solve the general quintic.

10 Apr

Solvable Quintics, Part 2

Posted by tpiezas in algebra, equations, mathematics. Tagged: , .

In the 1850’s, Jerrard showed that a Tschirnhausen transformation could reduce in radicals the general quintic into one missing three terms,

\text{(1)}\;\; x^5+5ax+4b = 0

In 1864, Bring independently would do the same. It is now known as the Bring-Jerrard quintic.  Such a reduction is important because it proved that a formula for the general quintic does exist, albeit it went beyond radicals and used elliptic functions, as was first done by Hermite.

In 1885, Runge et al showed that all solvable quintics [1] with rational coefficients have the form,

x^5+5\,\frac{4u+3}{u^2+1}xz^4+4\,\frac{(2u+1)(4u+3)}{u^2+1}z^5 = 0

A century later, Spearman and Williams gave their version,

x^5+5\,\frac{4v+3}{v^2+1}xz^4+4\,\frac{-2v+11}{\,v^2+1}z^5 = 0

So which is it? It turns out they are two sides of the same coin. Using the Spearman-Williams parametrization, let,

a = \frac{4v+3}{v^2+1}z^4

b = \frac{-2v+11}{\,v^2+1}z^5

and eliminating v between them using resultants, one gets,

\text{(2)}\;\; 4az^6+8bz^5-5a^2z^2+2abz-b^2 = 0

This is one of the simplest sextic resolvents for the quintic:  given {a, b}, if one can solve for z, then [1] is solvable. Since [2] is only a quadratic for b, we can easily solve for it,

b = az+4z^5+2z\sqrt{(a+z^4)(-a+4z^4)}

Still let,

a= \frac{4v+3}{v^2+1}z^4

and substituting it into the positive case of the square root yields the b of the 1885 version, while the negative case gives the b of the 1994 one, proving that they are indeed two sides of the same coin.

9 Apr

A Family of Solvable Quintics and Septics

Posted by tpiezas in algebra, equations, mathematics, Uncategorized. Tagged: , , .

Define,

x = \frac{-\sqrt{2}\,\eta(2\tau)}{\zeta_{48}\,\eta(\tau)}

where \eta is the Dedekind eta function, and \zeta_{48} is the 48th root of unity.  Then for \tau = \frac{1+\sqrt{-d}}{2} for d = {47, 103}, x is a root of the quintics,

x^5-2x^4+2x^3-x^2+1 = 0

x^5-2x^4+3x^3-3x^2+x+1 = 0

respectively. Note that the class number h(d) of both is 5.  It turns out these belong to a family of solvable quintics found by Kondo and Brumer,

x^5-2x^4+2x^3-x^2+1 = nx(x-1)^2

for any n, and where the two examples are n = {0, -1}.  A similar one for septics can be deduced from the examples in Kluner’s A Database For Number Fields as,

x^7-2x^6+x^5-x^4-5x^2-6x-4 = n(x-1)x^2(x+1)^2

with discriminant,

d = 4^4(4n^3+99n^2+34n+467)^3 .

The case n = 0 implies d = 467 and, perhaps not surprisingly, the class number of h(-467) = 7. However, since 467 does not have form 8m+7, then the eta quotient will be not be an algebraic number of degree h(-d).

To find a solvable family, it’s almost as if all you need is to find one right solvable equation, affix the right n-multiple of a polynomial on the RHS, and the whole family will remain solvable.

9 Apr

Solvable quintics

Posted by tpiezas in algebra, equations, mathematics. Tagged: , , .

Here is a nifty sufficient but not necessary condition on whether a quintic is solvable in radicals or not.  Given,

[1]  x^5+10cx^3+10dx^2+5ex+f = 0

If there is an ordering of its roots such that,

[2]  x_1 x_2 + x_2 x_3 + x_3 x_4 + x_4 x_5 + x_5 x_1 - \\(x_1 x_3 + x_3 x_5 + x_5 x_2 + x_2 x_4 + x_4 x_1) = 0

or alternatively, its coefficients are related by,

[3]  -25c^6-40c^3d^2-16d^4+35c^4e+\\28cd^2 e -11c^2e^2+e^3-2c^2df-2def+cf^2 = 0

then [1] is solvable as,

x = z_1^{1/5}+z_2^{1/5}+z_3^{1/5}+z_4^{1/5}

where the z_i are the roots of the simple quartic,

z^4+fz^3+(2c^5-5c^3e-4d^2e+ce^2+2cdf)z^2-c^5fz+c^{10} = 0

Note that [3] in fact is the constant term of Cayley’s resolvent sextic and is only quadratic in f.  Using another relation among the x_i, Dummit’s resolvent has a constant term that is already a quartic in f, hence the choice of relation matters.

Example 1: This family of quintics by this author satisfies [3],

x^5+10x^3+5(n^2+3n+18)x^2-5(n^3+n^2+15n-14)x+\\(n^4-n^3+37n^2+441) = 0

Let n = 1, and we have,

x^5+10x^3+110x^2-15x+478 = 0

Quartic is,

z^4+478z^3+11994z^2-478z+1 = 0

such that,

x = z_1^{1/5}+z_2^{1/5}+z_3^{1/5}+z_4^{1/5} = -4.50991\dots

Example 2: Another good example of [3] is Emma Lehmer’s quintic,

y^5 +n^2y^4-(2n^3+6n^2+10n+10)y^3+\\(n^4+5n^3+11n^2+15n+5)y^2+(n^3+4n^2+10n+10)y+1

The linear transformation,

y = x-n^2/5

will reduce it into the form of [1], and it will then be seen its coefficients obey [3]. As a particular example, let n = 5 and we have the reduced form,

x^5-710x^3+11005x^2-59640x+108701 = 0

Let its roots be,

(x_1, x_2, x_3, x_4, x_5) \approx (-33.15,\; 4.83,\; 12.16,\; 4.99,\; 11.16)

and we find that indeed it obeys [2].

Unfortunately, no similar simple relation between the coefficients of a solvable septic, or 7th degree equation, is yet known.

5 Apr

The Brioschi quintic and the Rogers-Ramanujan continued fraction

Posted by tpiezas in algebra, equations, geometry, mathematics. Tagged: , , , .

Given Ramanujan’s constant,

e^{\pi\sqrt{163}} \approx Q+743.9999999999992\dots

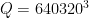where Q = 640320^3, why do we know, in advance, that the quintic,

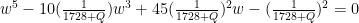
w^5-10(\frac{1}{1728+Q})w^3+45(\frac{1}{1728+Q})^2w-(\frac{1}{1728+Q})^2 = 0

is solvable in radicals?  The answer is this: The general quintic can be transformed in radicals to the one-parameter form,

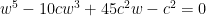
w^5-10cw^3+45c^2w-c^2 = 0

called the Brioschi quintic.  Whether reducible or not, if it is solvable in radicals and c is rational, then it can be shown c must have the form,

c = 1/(1728-t)

where,

t = \frac{(u^2+10u+5)^3}{u}

for some radical u. (For example, u = 1 will yield an irreducible though solvable quintic.)  But it seems Nature likes to recycle polynomials as this is also one of the many formulas for the j-function j(\tau), namely,

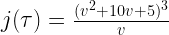
j(\tau) = \frac{(v^2+10v+5)^3}{v}

where,

v = \Big(\frac{\sqrt{5}\,\eta(5\tau)}{\eta(\tau)}\Big)^6

and \eta(\tau) is the Dedekind eta function.  However, if we let,

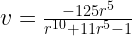
v = \frac{-125r^5}{r^{10}+11r^5-1}

then we get the more well-known j-function formula,

j(\tau) = \frac{-(r^{20}-288r^{15}+494r^{10}+228r^5+1)^3}{r^5(r^{10}+11r^5-1)^5}

where the numerator and denominator are polynomial invariants of the icosahedron,

a Platonic solid wherein one can find pentagons (which, of course, has 5 sides).  Perhaps not surprisingly, r is given by the eta quotient,

r^{-1}-r = \frac{\eta(\tau/5)}{\eta(5\tau)}+1

But one can also express r using the beautiful Rogers-Ramanujan continued fraction. Let,

q = e^{2 \pi i \tau}

then,

r = r(\tau) = \cfrac{q^{1/5}}{1+ \cfrac{q}{1 + \cfrac{q^2}{1+ \cfrac{q^3}{1 + \ddots}}}}

One of the simplest cases is,

r(\sqrt{-1}) = 5^{1/4}\sqrt{\frac{1+\sqrt{5}}{2}}-\frac{1+\sqrt{5}}{2}= \cfrac{e^{-2\pi/5}}{1+ \cfrac{e^{-2\pi}}{1 + \cfrac{e^{-4\pi}}{1+ \cfrac{e^{-6\pi}}{1 + \ddots}}}} \approx 0.284079

which was communicated by Ramanujan to Hardy in his famous letter.

Interesting, isn’t it?

For a related topic, kindly read “Ramanujan’s Continued Fractions and the Platonic Solids“.

4 Apr

An Icosahedral and Brioschi quintic identity

Posted by tpiezas in algebra, equations, mathematics. Tagged: , .

Here’s an identity I found.  For arbitrary r, define,

a = \frac{r^5(r^{10}+11r^5-1)^5}{(r^{30}+522r^{25}-10005r^{20}-10005r^{10}-522r^5+1)^2}

and,

w = \frac{r^2(r^{10}+11r^5-1)^2(r^6+2r^5-5r^4-5r^2-2r+1)}{r^{30}+522r^{25}-10005r^{20}-10005r^{10}-522r^5+1}

then,

w^5-10aw^3+45a^2w-a^2 = 0

Those two complicated expressions neatly wrap up into that last equation, doesn’t it?  This is the Brioschi quintic form which the general quintic can be reduced into.  Two of the polynomials are easily recognizable as icosahedral invariants, while,

P(r) = r^6+2r^5-5r^4-5r^2-2r+1

is a polynomial invariant for the octahedron. This gave rise to the question here.