continued fractions

Posts Tagged ‘continued fractions’

23 Jul

Hypergeometric formulas for Ramanujan’s continued fractions 2

Posted by tpiezas in complex analysis, geometry, identities. Tagged: continued fractions, hypergeometric function, quintics, Ramanujan. 2 comments

(continued from yesterday’s post)

III. Icosahedral group

Given the Rogers-Ramanujan identities (see also here),

$\begin{aligned} G(q) &= \sum_{n=0}^\infty \frac{q^{n^2}}{(q;q)_n} = \prod_{n=1}^\infty \frac{1}{(1-q^{5n-1})(1-q^{5n-4})}\\H(q) &= \sum_{n=0}^\infty \frac{q^{n^2+n}}{(q;q)_n} = \prod_{n=1}^\infty \frac{1}{(1-q^{5n-2})(1-q^{5n-3})}\end{aligned}$

I observed that,

$\begin{aligned}&q^{-1/60}G(q) = j^{1/60}\,_2F_1\big(\tfrac{19}{60},\tfrac{-1}{60},\tfrac{4}{5},\tfrac{1728}{j}\big) = (j-1728)^{1/60}\,_2F_1\big(\tfrac{29}{60},\tfrac{-1}{60},\tfrac{4}{5},\tfrac{1728}{1728-j}\big)\\[2.5mm]&q^{11/60}H(q) = j^{-11/60}\,_2F_1\big(\tfrac{31}{60},\tfrac{11}{60},\tfrac{6}{5},\tfrac{1728}{j}\big) = (j-1728)^{-11/60}\,_2F_1\big(\tfrac{41}{60},\tfrac{11}{60},\tfrac{6}{5},\tfrac{1728}{1728-j}\big)\end{aligned}$

where, as in the previous post, $j=j(\tau)$ is the j-function, $q = e^{2\pi i \tau} = \exp(2\pi i \tau)$ , $\tau = \sqrt{-N}$ , and $N>1$ . Since it is known that,

$\begin{aligned}&r(q) = \cfrac{q^{1/5}}{1 + \cfrac{q}{1 + \cfrac{q^2}{1 + \cfrac{q^3}{1 + \ddots}}}} = \frac{q^{11/60}H(q)}{q^{-1/60}G(q)} = \frac{q^{11/60}\prod_{n=1}^\infty \frac{1}{(1-q^{5n-2})(1-q^{5n-3})}}{q^{-1/60}\prod_{n=1}^\infty \frac{1}{(1-q^{5n-1})(q^{5n-4})}}\end{aligned}$

this implies that,

$\begin{aligned}r(q) &=\frac{j^{-11/60}\,_2F_1\big(\frac{31}{60},\frac{11}{60},\frac{6}{5},\frac{1728}{j}\big) }{j^{1/60}\,_2F_1\big(\frac{19}{60},\frac{-1}{60},\frac{4}{5},\frac{1728}{j}\big)}\\[3mm]&=\frac{(j-1728)^{-11/60}\,_2F_1\big(\frac{41}{60},\frac{11}{60},\frac{6}{5},\frac{1728}{1728-j}\big) }{(j-1728)^{1/60}\,_2F_1\big(\frac{29}{60},\frac{-1}{60},\frac{4}{5},\frac{1728}{1728-j}\big)}\end{aligned}$

Example. Let $\tau = \sqrt{-4}$ , hence $j = j(\sqrt{-4}) = 66^3$ . Then,

$1/r(q) -r(q) = \left(\frac{1+\sqrt{5}}{2}\right)^4+\left(\frac{1+\sqrt{5}}{2}\right)5^{3/4} = 12.2643\dots$

Furthermore, since Ramanujan established that,

$G(q^{11})H(q)-q^2G(q)H(q^{11}) = 1$

if we define the two functions,

$\begin{aligned}U(\tau) &= \big(j(\tau)\big)^{1/60}\,_2F_1\big(\tfrac{19}{60},\tfrac{-1}{60},\tfrac{4}{5},\tfrac{1728}{j(\tau)}\big)\\V(\tau) &= \big(j(\tau)\big)^{-11/60}\,_2F_1\big(\tfrac{31}{60},\tfrac{11}{60},\tfrac{6}{5},\tfrac{1728}{j(\tau)}\big) \end{aligned}$

then the counterpart hypergeometric identity is also beautifully simple and given by,

$U(11\tau)V(\tau)-U(\tau)V(11\tau)=1$

In the next post, we will use one of the hypergeometric formulas to solve the general quintic.

22 Jul

Hypergeometric formulas for Ramanujan’s continued fractions 1

Posted by tpiezas in complex analysis, geometry, mathematics. Tagged: continued fractions, hypergeometric function, j-function, Ramanujan. 1 comment

There are five Platonic solids, two are duals to another two, while the tetrahedron is self-dual. As such, this gives rise to 3 polyhedral groups: the tetrahedral group of order 12, the octahedral group of order 24, and the icosahedral group of order 60.

Amazingly, Ramanujan found 3 continued fractions that can be associated with each group. See this article for more details. It turns out there are also corresponding hypergeometric formulas, and the numbers 12, 24, and 60 naturally appears.

First though, define the j-function as,

$j = j(\tau) = \frac{1}{q} + 744 + 196884q + 21493760q^2 + \dots$

where,

$q = e^{2\pi i \tau} = \exp(2\pi i \tau)$

This can be conveniently calculated in Mathematica as,

$j(\tau) = 1728\text{KleinInvariantJ}(\tau)$

NOTE: In the formulas below, it will be assumed that,

$\tau = \sqrt{-N},\;\; N > 1$

I. Tetrahedral group

Given,

$\begin{aligned}&c=c(q)=\cfrac{q^{1/3}}{1 + \cfrac{q+q^2}{1 + \cfrac{q^2+q^4}{1 + \cfrac{q^3+q^6}{1 + \ddots}}}} = q^{1/3}\prod_{n=1}^\infty \frac{(1-q^{6n-1})(1-q^{6n-5})}{(1-q^{6n-3})^2}\end{aligned}$

and,

$\begin{aligned}&d = j^{1/3}\,\frac{\,_2F_1\big(\frac{1}{4},\frac{-1}{12},\frac{2}{3},\frac{1728}{j}\big)}{\,_2F_1\big(\frac{1}{4},\frac{7}{12},\frac{4}{3},\frac{1728}{j}\big)}\end{aligned}$

then we have the simple relationship,

$d = 4c^2+c^{-1}$

Example. Let $\tau = \sqrt{-2}$ , hence $j=j(\sqrt{-2}) = 20^3$ , then,

$d = 3\sqrt{2(11+4\sqrt{6})} = 19.3484\dots$

and c(q) can then be easily solved for as a cubic equation.

II. Octahedral group

Let,

$\begin{aligned}&u = u(q) = \cfrac{\sqrt{2}\,q^{1/8}}{1 + \cfrac{q}{1+q + \cfrac{q^2}{1+q^2 + \cfrac{q^3}{1+q^3 + \ddots}}}} = \sqrt{2}\,q^{1/8}\prod_{n=1}^\infty\frac{1-q^{2n-1}}{(1-q^{4n-2})^2} \end{aligned}$

then,

$\begin{aligned}&u = \frac{\sqrt{2}}{j^{1/8}}\left(\frac{\,_2F_1\big(\frac{5}{24},\frac{13}{24},\frac{5}{4},\frac{1728}{j}\big)}{\,_2F_1\big(\frac{7}{24},\frac{-1}{24},\frac{3}{4},\frac{1728}{j}\big)}\right)^{1/2}\end{aligned}$

Example. Still using $\tau = \sqrt{-2}$ , then,

$u = \sqrt{1+\sqrt{2}-\sqrt{2(1+\sqrt{2})}} = 0.4656\dots$

III. Icosahedral group

(To be discussed in the next post.)

7 May

Ramanujan’s continued fraction for Catalan’s constant

Posted by tpiezas in algebra, mathematics, number theory. Tagged: constants, continued fractions, Ramanujan. Leave a comment

Ramanujan was a goldmine when it came to continued fractions (and many others). In this post, two families will be given: they involve pi and Catalan’s constant as special cases. However, versions will be given that roughly double the rate of convergence.

Recall that Catalan’s constant C is given by,

$C = \sum_{n=0}^\infty \frac{(-1)^n}{(2n+1)^2} = 0.915965\dots$

Ramanujan gave the beautiful pair of continued fractions. Let $|x| > 1$ , then,

$f(x) = 2\sum_{n=0}^\infty \frac{(-1)^n}{(x+2n+1)^2} = \cfrac{1}{x^2-1 + \cfrac{2^2}{1 + \cfrac{2^2}{x^2-1 + \cfrac{4^2}{1 + \cfrac{4^2}{x^2-1 +\ddots}}}}}$

$g(x) \; = \;\frac{\Gamma^4 (\frac{x+1}{4})}{\Gamma^4 (\frac{x+3}{4})}\; =\; \cfrac{16}{x^2-1 + \cfrac{1^2}{1 + \cfrac{1^2}{x^2-1 + \cfrac{3^2}{1 + \cfrac{3^2}{x^2-1 +\ddots}}}}}$

One can just admire Ramanujan’s artistry — one continued fraction uses even numerators, the other, odd numerators. For even x > 0, it is easily seen the first one involves Catalan’s constant. For example,

$f(2) = 2(1-C)$

On the other hand, for odd x > 1, both involve pi,

$f(3) = \frac{1}{24}(12-\pi^2)$

$g(3) = \pi^2$

Notice though that numerators are repeated. Thanks to the insight of J.M. from a mathstackexchange post about Apery’s constant, we can speed up the rate of convergence of this particular form by getting rid of every other level and extracting even convergents. After some slightly tedious algebraic manipulation, given,

$y = \cfrac{a_1}{b_1 + \cfrac{a_2}{1 + \cfrac{a_3}{b_2 + \cfrac{a_4}{1 +\ddots}}}}$

then,

$y_{even} = \cfrac{a_1}{b_1+a_2 - \cfrac{a_2\, a_3}{b_2+a_3+a_4 - \cfrac{a_4\, a_5}{b_3+a_5+a_6 - \cfrac{a_6\, a_7}{b_4+a_7+a_8 -\ddots}}}}$

So Ramanujan’s continued fractions are now the more compact,

$f(x) = 2\sum_{n=0}^\infty \frac{(-1)^n}{(x+2n+1)^2} = \cfrac{1}{u_1 - \cfrac{2^4}{u_2 - \cfrac{4^4}{u_3 - \cfrac{6^4}{u_4 -\ddots}}}}$

where, starting with n = 1,

$u_n = (2n-2)^2 + (2n)^2 + x^2-1$

and,

$g(x) \; = \; \frac{\Gamma^4 (\frac{x+1}{4})}{\Gamma^4(\frac{x+3}{4})}\; =\; \cfrac{16}{-1+v_1 - \cfrac{1^4}{v_2 - \cfrac{3^4}{v_3 - \cfrac{5^4}{v_4 -\ddots}}}}$

$v_n = (2n-3)^2 + (2n-1)^2 + x^2-1$

Thus, we have the slightly faster continued fraction for Catalan’s constant C,

$f(2) = 2(1-C) = \cfrac{1}{u_1 - \cfrac{2^4}{u_2 - \cfrac{4^4}{u_3 - \cfrac{6^4}{u_4 -\ddots}}}}$

where,

$u_n = 8n^2-8n+7$

(There is an even faster one by Zudilin given in An Apery-like difference equation for Catalan’s constant though he states this still does not prove C is irrational.)

6 May

Zudilin’s continued fraction for Zeta(4)

Posted by tpiezas in equations, mathematics, number theory, sequences. Tagged: continued fractions, Riemann zeta function, sequences. 1 comment

Euler proved the following general continued fraction formula,

$\frac{1}{u_1}+\frac{1}{u_2}+\frac{1}{u_3} = \cfrac{1}{u_1 - \cfrac{u_1^2}{u_1+u_2 - \cfrac{u_2^2}{u_2+u_3 - \cfrac{u_3^2}{u_3+u_4 - \ddots}}}}$

which automatically gives a representation for the Riemann zeta function $\zeta(s)$ . However, the convergence is rather slow. Apery found a much faster version for $\zeta(3)$ and proved its irrationality. The status for other odd s, however, remains open. While it has already been proved irrational for all even s, Wadim Zudilin nonetheless found an interesting faster version for $\zeta(4)$ .

First, consider the following known binomial sums,

$\sum_{n=1}^\infty \frac{1}{n\,\binom{2n}n} = \frac{1}{3\sqrt{3}}\,\pi$

$\sum_{n=1}^\infty \frac{1}{n^2\,\binom{2n}n} = \frac{1}{3}\,\zeta(2)$

$\sum_{n=1}^\infty \frac{(-1)^{n+1}}{n^3\,\binom{2n}n} = \frac{2}{5}\,\zeta(3)$

$\sum_{n=1}^\infty \frac{1}{n^4\,\binom{2n}n} = \frac{17}{36}\,\zeta(4)$

This nice pattern stops at s = 4. (There are sums for other s, but they do not have this succinct form.) It is suggestive then that $\zeta(4)$ belongs to the same family and may share certain similarities.

Zudilim found that,

$\zeta(4) = \cfrac{13}{p_0 + \cfrac{1^8\, q_1}{p_1+ \cfrac{2^8\,q_2}{p_2+\cfrac{3^8\,q_3}{p_3 + \ddots}}}}$

where, starting with n = 0,

$p_n = 3(2n+1)(3n^2+3n+1)(15n^2+15n+4) = 12, 2142, 26790, 142968,\dots$

$q_n = 3(3n-1)(3n+1) = -3, 24, 105, 240, 429\dots$

(Note that the cfrac does not use $q_0$ .) Like Apery’s accelerated version for $\zeta(2)$ , the partial denominators use addition, in contrast to Euler’s form which has subtraction. Also, like its siblings, it obeys a recurrence relation,

$(n+1)^5U_{n+1}=p_n U_n+n^3q_nU_{n-1}$

Starting with $U_0=1, U_1=12$ , one gets the sequence,

$U_n = 1, 12, 804, 88680, \dots$

which is not yet in the OEIS. In Theorem 4, Zudilin mentions they are positive rationals, but some Mathematica experimentation will show that apparently all the $U_i$ are integral. (Proof anyone?) Furthermore, they have the limit,

$\lim_{n \to \infty} \frac{U_{n+1}}{U_n} = (3+2\sqrt{3})^3$

For more details, refer to Zudilin’s An Apery-like difference equation for Catalan’s constant. Now if only someone will do something more about $\zeta(5)$ …

6 May

The silver ratio and a continued fraction for log(2)

Posted by tpiezas in mathematics, number theory, sequences. Tagged: continued fractions, logarithm, quadratic. Leave a comment

Define the three sequences,

$C_n = \sum_{k=0}^n {\binom n k} {\binom {n+k}k} = 1, 3, 13, 63, 321,\dots$

$B_n = \sum_{k=0}^n {\binom n k}^2 {\binom {n+k}k} = 1, 3, 19, 147, 1251,\dots$

$A_n = \sum_{k=0}^n {\binom n k}^2 {\binom {n+k}k}^2 = 1, 5, 73, 1445, 33001, \dots$

The last two are Apery numbers and have been discussed previously. The first are the central Delannoy numbers which obeys the limit,

$\lim_{n \to \infty} \frac{C_{n+1}}{C_n} = \left(1+\sqrt{2}\right)^2 = 5.8284\dots$

which is the square of the silver ratio. (The ratios for the others have already been mentioned.) These have the recurrence relations,

$n C_n = 3(2n-1)C_{n-1}-(n-1)C_{n-2}$

$n^2 B_n = (11n^2-11n+3)B_{n-1}+(n-1)^2B_{n-2}$

$n^3 A_n = (34n^3-51n^2+27n-5)A_{n-1}-(n-1)^3A_{n-2}$

To recall, the polynomials $P(n) =11n^2-11n+3$ and $P(n) = 34n^3-51n^2+27n-5$ generated numbers for the continued fractions of $\zeta(2), \zeta(3)$ , so I was curious if $P(n) = 3(2n-1)$ could be used in an analogous manner. It turns out, depending on what sign to use, it gives either $\log(2)$ or $\arctan(\frac{1}{3})$ ,

$\frac{1}{2}\log(2) = \cfrac{1}{v_1 - \cfrac{1^2}{v_2 - \cfrac{2^2}{v_3 - \cfrac{3^2}{v_4-\ddots}}}}$

or,

$\arctan(\frac{1}{3}) = \cfrac{1}{v_1 + \cfrac{1^2}{v_2 + \cfrac{2^2}{v_3 + \cfrac{3^2}{v_4 + \ddots}}}}$

where, starting with n = 1,

$v_n = 3(2n-1)$

This can be partly demystified since one continued fraction for the natural logarithm, and arctan, is,

$\frac{1}{2}\log\left(1+\frac{2x}{y}\right)= \cfrac{x}{1(x+y) - \cfrac{(1x)^2}{3(x+y) - \cfrac{(2x)^2}{5(x+y) - \cfrac{(3x)^2}{7(x+y) - \ddots}}}}$

and,

$\arctan(\frac{x}{z}) = \cfrac{x}{1z + \cfrac{(1x)^2}{3z + \cfrac{(2x)^2}{5z + \cfrac{(3x)^2}{7z + \ddots}}}}$

Hence, if $x+y = z$ , as with the case {x, y, z} = {1, 2, 3}, then there will be identical-looking continued fractions that differ only in the signs. But it remains interesting how the recurrence relations of these three binomial sums are involved in the continued fractions of $\log(2), \zeta(2), \zeta(3)$ . Later, we shall see there is a recurrence relation for the cfrac of $\zeta(4)$ as well.

4 May

A new continued fraction for Zeta(3)?

Posted by tpiezas in equations, mathematics, number theory. Tagged: continued fractions, pi, Riemann zeta function. Leave a comment

Continuing the discussion from the previous post, Ramanujan also gave a continued fraction for $\zeta(3)$ as,

$\zeta(3) = 1+\cfrac{1}{u_1+\cfrac{1^3}{1+\cfrac{1^3}{u_2+\cfrac{2^3}{1+\cfrac{2^3}{u_3 + \ddots}}}}}$

where the $u_n$ , starting with n = 1, are given by the linear function,

$u_n = 4(2n-1) = 4, 12, 20, 28, \dots$

(Notice the difference from the other version since this one has the cubes twice used as numerators.) Using a similar approach to Apery’s of finding a faster converging version, I found via Mathematica that,

$\zeta(3) = \cfrac{6}{v_1 + \cfrac{1^3}{1 + \cfrac{1^3}{v_2 + \cfrac{2^3}{1 + \cfrac{2^3}{v_3 +\ddots}}}}}$

where the $v_n$ are now given by the cubic function,

$v_n = 4(2n-1)^3 = 4, 108, 500, 1372, \dots$

Of course, a more rigorous mathematical proof is needed that indeed the equality holds.

Update: J.M. from mathstackexchange.com proved that the continued fraction DOES converge to $\zeta(3)$ by connecting it to Apery’s version! One consequence of his analysis is that Apery’s generating polynomial can be seen as,

$(2n-1)(17n^2-17n+5) = n^3 + (n-1)^3 + 4(2n-1)^3$

4 May

Continued fractions for Zeta(2) and Zeta(3)

Posted by tpiezas in algebra, equations, mathematics, number theory. Tagged: continued fractions, pi, Ramanujan, Riemann zeta function. 2 comments

It seems there is a nice “pattern” between the continued fractions for the Riemann zeta function,

$\zeta(s) = \sum_{n=1}^\infty \frac{1}{n^s} = \frac{1}{1^s}+\frac{1}{2^s}+\frac{1}{3^s}+\dots$

at s = 2, and s = 3. First though, a little introduction.

The origins of this function go back to 1644 when, at the tender age of 18, the Italian mathematician Pietro Mengoli (1626-1686) first proposed what would be later known as the Basel Problem, namely to determine the exact value of the sum of the reciprocals of the squares. Euler would later find that, for n a positive integer, then 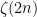$\zeta(2n)$ is a rational multiple of 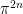$\pi^{2n}$ , with the first case s = 2 as,

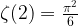
$\zeta(2) = \frac{\pi^2}{6}$

which obviously is irrational. However, the status of odd s was not as easy to resolve. It was only in 1979 that Apery proved that 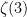$\zeta(3)$ is irrational, which henceforth was called Apery’s constant.

I. Zeta(2)

One of its infinite number of continued fractions can be given as,

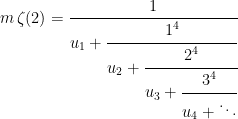
$m\,\zeta(2) = \cfrac{1}{u_1+\cfrac{1^4}{u_2+\cfrac{2^4}{u_3+\cfrac{3^4}{u_4+\ddots}}}}$

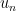where $m = \frac{1}{2}$ and the $u_n$ , starting with n = 1, are generated by,

$u_n = 2n-1 = 1, 3, 5, 7,\dots$

or simply the odd numbers. The convergence is slow, but Apery found it can accelerated by using a quadratic function,

$u_n = 11n^2-11n+3 = 3, 25, 69, 135,\dots$

but now $m = \frac{1}{5}$ .

II. Zeta(3)

Likewise, this also has an infinite number of continued fractions (see Ramanujan’s versions here), but one important form is,

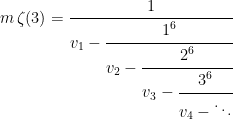
$m\,\zeta(3) = \cfrac{1}{v_1-\cfrac{1^6}{v_2-\cfrac{2^6}{v_3-\cfrac{3^6}{v_4-\ddots}}}}$

where 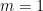$m = 1$ and the 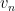$v_n$ , again starting with n = 1, are,

$v_n = (n-1)^3+n^3 = (2n-1)(n^2-n+1) = 1, 9, 35, 91, \dots$

Apery again found an accelerated version,

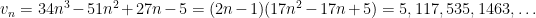
$v_n = 34n^3-51n^2+27n-5 = (2n-1)(17n^2-17n+5) = 5, 117, 535, 1463, \dots$

where now 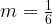$m = \frac{1}{6}$ , and established that its rate of convergence was such that 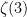$\zeta(3)$ could not be a ratio of two integers.

III. Connection between Zeta(2) and Zeta(3)

Define the two sequences,

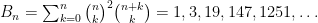
$B_n = \sum_{k=0}^n {\binom n k}^2 {\binom {n+k}k} = 1, 3, 19, 147, 1251,\dots$

$A_n = \sum_{k=0}^n {\binom n k}^2 {\binom {n+k}k}^2 = 1, 5, 73, 1445, 33001, \dots$

then it was established that these Apery numbers have the recurrence relations,

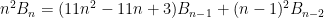
$n^2 B_n = (11n^2-11n+3)B_{n-1}+(n-1)^2B_{n-2}$

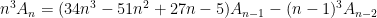
$n^3 A_n = (34n^3-51n^2+27n-5)A_{n-1}-(n-1)^3A_{n-2}$

Interesting that the same polynomials pop up, isnt’ it? Furthermore, their limiting ratios have the common form,

$\left(\frac{b+\sqrt{b^2+4}}{2}\right)^{6-b}$

thus for b = 1, 2,

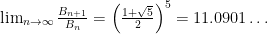
$\lim_{n \to \infty} \frac{B_{n+1}}{B_n} = \left(\frac{1+\sqrt{5}}{2}\right)^5 = 11.0901\dots$

$\lim_{n \to \infty} \frac{A_{n+1}}{A_n} = \left(1+\sqrt{2}\right)^4 = 33.9705\dots$

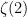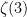hence the golden ratio and the silver ratio surprisingly turn up in the continued fractions for $\zeta(2)$ and $\zeta(3)$ , respectively. It is easy to check other sequences,

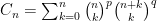
$C_n = \sum_{k=0}^n {\binom n k}^p {\binom {n+k}k}^q$

for some small {p, q}, but there are no other recurrence relations similar in form to the two above.

IV. Zeta(5)

There is an orderly non-simple continued fraction for all 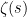$\zeta(s)$ , with the next odd s as,

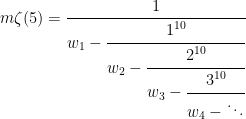
$m \zeta(5) = \cfrac{1}{w_1-\cfrac{1^{10}}{w_2-\cfrac{2^{10}}{w_3-\cfrac{3^{10}}{w_4-\ddots}}}}$

where 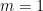$m = 1$ and the 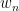$w_n$ are,

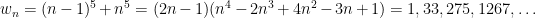
$w_n = (n-1)^5+n^5 = (2n-1)(n^4-2n^3+4n^2-3n+1) = 1, 33, 275, 1267, \dots$

Unfortunately, no one has yet found an accelerated version where the 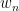$w_n$ are generated by a 5th degree (or higher) polynomial, and m is rational.

Can you find one?

For further reading, refer to Alfred van der Poorten’s excellent, A Proof That Euler Missed.

3 May

Some of Ramanujan’s continued fractions for pi

Posted by tpiezas in algebra, mathematics, number theory. Tagged: continued fractions, pi, Ramanujan. 1 comment

The digits of pi go on forever apparently with no discernible pattern. However, there are beautifully simple patterns in its (ironically) non-simple continued fraction expansions. Examples are,

$\pi = \cfrac{4}{1 + \cfrac{1^2}{2 + \cfrac{3^2}{2 + \cfrac{5^2}{2 + \ddots} }}}$

known by Lord Brouncker (1620-1684), and,

$\pi = 3 + \cfrac{1^2}{6 + \cfrac{3^2}{6 + \cfrac{5^2}{6 + \ddots} }}$

One can see the affinity between the two. They in fact belong to the same family. Given complex numbers {n, x} with $Re[x] > 0$ , then,

$F(n,x) = \Large{\frac{\Gamma\left(\frac{x+n+1}{4} \right)\Gamma\left(\frac{x-n+1}{4} \right) }{\Gamma\left(\frac{x+n+3}{4} \right)\Gamma\left(\frac{x-n+3}{4} \right)}} = \cfrac{4}{x + \cfrac{1^2-n^2}{2x + \cfrac{3^2-n^2}{2x + \cfrac{5^2-n^2}{2x + \ddots} }}}$

where $\Gamma(\tau)$ is the gamma function. This is Entry 25 in Ramanujan’s Second Notebook (Chapter 12) though this result was also known by Euler. For the case n = 0, the continued fraction assumes the form of the examples and the function simplifies as,

$F(0,x) = \frac{\Gamma^2\left(\frac{x+1}{4}\right)}{\Gamma^2\left(\frac{x+3}{4}\right)}$

For x an odd integer, then F (0, x) is a rational multiple of $\pi$ or $1/\pi$ . Specifically, for x = {1, 3, 5, 7, 9}, we have,

$F(0,x) = \pi,\; \frac{4}{\pi}, \frac{\pi}{4}, \frac{16}{9\pi}, \frac{9\pi}{64}$

More generally,

$F(0,4m+1) = \big(\frac{(2m)!}{m!^2}\big)^2\, \frac{\pi}{2^{4m}}$

$F(0,4m+3) = \big(\frac{m!^2}{(2m+1)!}\big)^2\, \frac{2^{4m+2}}{\pi}$

See p. 178 of Annie Cuyt’s HandBook of Continued Fractions for Special Functions. For more examples, see also this article Ramanujan’s Continued Fractions, Apery’s Constant, and more.

5 Apr

The Brioschi quintic and the Rogers-Ramanujan continued fraction

Posted by tpiezas in algebra, equations, geometry, mathematics. Tagged: continued fractions, j-function, quintics, Ramanujan. Leave a comment

Given Ramanujan’s constant,

$e^{\pi\sqrt{163}} \approx Q+743.9999999999992\dots$

where $Q = 640320^3$ , why do we know, in advance, that the quintic,

$w^5-10(\frac{1}{1728+Q})w^3+45(\frac{1}{1728+Q})^2w-(\frac{1}{1728+Q})^2 = 0$

is solvable in radicals? The answer is this: The general quintic can be transformed in radicals to the one-parameter form,

$w^5-10cw^3+45c^2w-c^2 = 0$

called the Brioschi quintic. Whether reducible or not, if it is solvable in radicals and c is rational, then it can be shown c must have the form,

$c = 1/(1728-t)$

where,

$t = \frac{(u^2+10u+5)^3}{u}$

for some radical u. (For example, u = 1 will yield an irreducible though solvable quintic.) But it seems Nature likes to recycle polynomials as this is also one of the many formulas for the j-function $j(\tau)$ , namely,

$j(\tau) = \frac{(v^2+10v+5)^3}{v}$

where,

$v = \Big(\frac{\sqrt{5}\,\eta(5\tau)}{\eta(\tau)}\Big)^6$

and $\eta(\tau)$ is the Dedekind eta function. However, if we let,

$v = \frac{-125r^5}{r^{10}+11r^5-1}$

then we get the more well-known j-function formula,

$j(\tau) = \frac{-(r^{20}-288r^{15}+494r^{10}+228r^5+1)^3}{r^5(r^{10}+11r^5-1)^5}$

where the numerator and denominator are polynomial invariants of the icosahedron,

a Platonic solid wherein one can find pentagons (which, of course, has 5 sides). Perhaps not surprisingly, r is given by the eta quotient,

$r^{-1}-r = \frac{\eta(\tau/5)}{\eta(5\tau)}+1$

But one can also express r using the beautiful Rogers-Ramanujan continued fraction. Let,

$q = e^{2 \pi i \tau}$

then,

$r = r(\tau) = \cfrac{q^{1/5}}{1+ \cfrac{q}{1 + \cfrac{q^2}{1+ \cfrac{q^3}{1 + \ddots}}}}$

One of the simplest cases is,

$r(\sqrt{-1}) = 5^{1/4}\sqrt{\frac{1+\sqrt{5}}{2}}-\frac{1+\sqrt{5}}{2}= \cfrac{e^{-2\pi/5}}{1+ \cfrac{e^{-2\pi}}{1 + \cfrac{e^{-4\pi}}{1+ \cfrac{e^{-6\pi}}{1 + \ddots}}}} \approx 0.284079$

which was communicated by Ramanujan to Hardy in his famous letter.

Interesting, isn’t it?

For a related topic, kindly read “Ramanujan’s Continued Fractions and the Platonic Solids“.

tpiezas A Collection of Algebraic Identities

Posts Tagged ‘continued fractions’

Hypergeometric formulas for Ramanujan’s continued fractions 2

Hypergeometric formulas for Ramanujan’s continued fractions 1

Ramanujan’s continued fraction for Catalan’s constant

Zudilin’s continued fraction for Zeta(4)

The silver ratio and a continued fraction for log(2)

A new continued fraction for Zeta(3)?

Continued fractions for Zeta(2) and Zeta(3)

Some of Ramanujan’s continued fractions for pi

The Brioschi quintic and the Rogers-Ramanujan continued fraction

Recent Posts

Archives

Categories

Meta